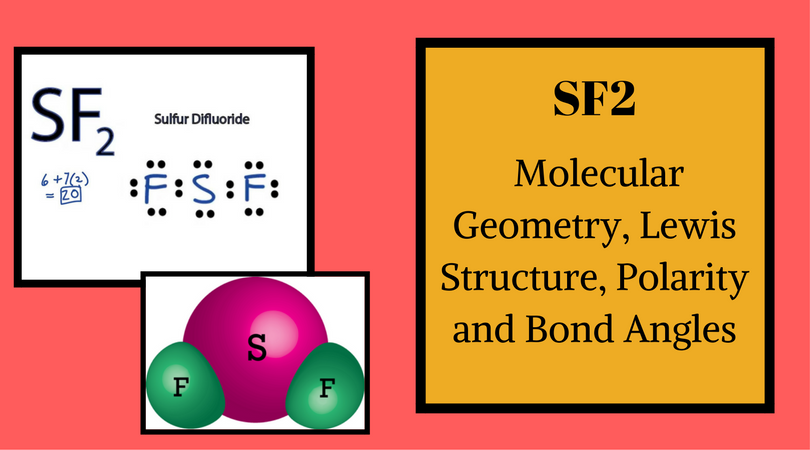
Sulfur Difluoride is an inorganic molecule made up of one Sulphur atom and two Fluorine atoms. It has a chemical formula of SF2 and can be generated by the reaction of Sulphur Dioxide and Potassium Fluoride or Mercury Fluoride. In this blog post, we will look at the Lewis dot structure of SF2, its molecular geometry and shape.
| Name of molecule | Sulfur Difluoride ( SF2) |
| No of Valence Electrons in the molecule | 20 |
| Hybridization of SF2 | sp3 hybridization |
| Bond Angles | 98 degrees |
| Molecular Geometry of SF2 | Bent |
Contents
SF2 Valence electrons
For drawing the Lewis structure for any molecule, we first need to know the total number of valence electrons. So we will first find out the total valence electrons for Sulphur Difluoride.
Total number of valence electrons for SF2 – Valence electrons of Sulphur + Valence electrons of Fluorine
Sulfur has six valence electrons in its outer shell.
Fluorine has seven valence electrons.
Total number of valence electrons for SF2 – 6 + 7*2 ( as there are two atoms of Fluorine, we will multiply the number by 2)
= 6 + 14
= 20 valence electrons
So, Sulphur Difluoride has a total of 20 valence electrons.
SF2 Lewis Structure
Lewis Structure is the pictorial representation of the arrangement of valence electrons around the individual atoms in the molecule. And now that we know the total valence electrons of SF2, we will start making the Lewis Dot Structure for this molecule.
Firstly, place the Sulphur atom in the centre as it is less electronegative than Fluorine. So it will be in the central position with both these Fluorine atoms on the terminal ends.
Fluorine atoms need one valence electron to complete its octet so it will share one valence electron of the Sulphur atom. So both the Fluorine atoms form a single bond with the Sulphur atom by sharing one valence electron of the Sulphur atom.
Each bond uses up two valence electrons so here four valence electrons are used from 20 valence electrons. As octets of Fluorine atoms are complete, put six valence electrons around each Fluorine atom. So a total of 16 valence electrons are used.
And Sulfur atom has four valence electrons that do not participate in bond formation and hence it is called lone pair or nonbonding pair of electrons. So in the Lewis Structure of SF2, there are single bonds between Sulphur and Fluorine atoms with two lone pairs of electrons on the central Sulphur atom.

SF2 Hybridization
To find out the Hybridization of this molecule, we will consider the two numbers of atoms and the total number of lone electron pairs bonded to the molecule. Here, if we look at the Sulphur atom, it is bonded with two atoms and has two electrons pairs. We get the final number 4, which corresponds to sp3 Hybridization. In fact, both Fluorine atoms are also sp3 hybridized. So, SF2 has sp3 Hybridization.
SF2 Molecular Geometry
The molecular geometry of the molecule depends on the Lewis structure and the arrangement of valence electrons in the structure. The sulfur atom has two bonding pairs of electrons and two nonbonding pairs of electrons that represent the VSEPR notion of AX2E2, which corresponds to an angular/non-linear or bent molecular geometry. So Sulfur Difluoride has a bent molecular geometry.
SF2 Shape
In the Lewis Structure of SF2, the central atom forms two bonds with two Fluorine atoms and has two lone pairs of electrons. The two lone pairs of electrons push the Fluorine atoms downwards due to the repulsive forces, and as a result, the shape of this molecule is bent.

Hence, SF2 is a bent-shaped molecule due to the presence of lone pairs on the Sulphur atom.
SF2 Bond Angles
The molecules with linear geometry have bond angles of 180 degrees but here as the shape of the molecule is bent due to the lone pairs on the Sulphur atom, both Fluorine atoms are pushed downwards, deviating the bond angle of F-S-F from 180 to 98 degrees.

Is SF2 polar or nonpolar?
To determine the polarity of any molecule, we check for the following factors:
- Presence of lone pairs
- The shape of the molecule
- The difference in electronegativities of atoms
- Net Dipole moment in the molecule
Sulfur Difluoride has a bent molecule geometry having two single bonds and two lone pairs of electrons. These lone pairs of electrons distort the shape of the molecule, and hence it is non-linear. As these lone pairs try to keep their repulsive forces minimal, they push down the Fluorine atoms.
Due to the presence of the lone pairs, there is symmetry in the molecule. And as a result, the charges will not be evenly distributed, increasing the chances of the polarity in the molecule.

When we compare Sulphur and Fluorine atoms’ electronegativities, the value of electronegativity of Sulphur is 2.58 and for Fluorine is 3.98. So here the difference of the electronegativities of both these atoms is much higher than 0.5, which makes the S-F bonds polar. And due to this vast difference in electronegativity, there will be a dipole moment between Sulphur and Fluorine atoms. The direction of the dipole moment will be from the Sulphur atom towards the Fluorine atom, as here Fluorine will try to pull the shared electrons to itself.
As this molecule is not linear, the dipole moments on both sides are not canceled out, resulting in the non-zero net dipole moment of the molecule. Hence, SF2 has poles in the molecule, where there are partial negative charges on the Fluorine atom and partial positive charges on the Sulfur atom which makes SF2 a polar molecule.
Concluding Remarks
To summarise this blog, we can say that,
- SF2 has a simple Lewis structure in which the Sulphur atom is in the centre forming single bonds with both the Fluorine atoms.
- There are two lone pairs of electrons on the Sulphur atom which makes the geometry of the molecule bent.
- The Sulphur atom has sp3 Hybridization, and the bond angle of F-S-F is 98 degrees.
- It is a polar molecule as there is a net dipole moment in the molecule.




Can you please say this is planar or not??
No, SF2 hsd bent shape as there are two atoms bonded to the central atom as well as there are two lone pairs in it.
The molecular geometry of sf2 is a bent.
Interesting post
Really helps…